La Majestuosidad de Scholes!

¿Manchester y Chelsea los mejores Equipos del Mundo?

Mapas de Karnaugh

Maurice Karnaugh

Nació el 4 de octubre de 1924 en New York. Fue un Físico americano que tuvo como principal aporte la creación de los Mapas de Karnaugh o Diagrama de Veitch, cuya función es la de minimizar funciones algebráicas booleanas.

Mapas de Karnaugh

los mapas de carnaugh solo pueden ser utilizados hasta 5 variables.

ejercicios de como se resuelve un mapa de carnaugh:

Open Sourse o Codigo Abierto

Open Source

Esto es el Código abierto asi se le llama al software libre. los usuarios del software libre usan este nombre para tratar de cambiar el antiguo que es (free software).

Debido a que free sigifica en ingles muchas cosas como: gratuito,libre,pero no da nada referido al software que hay que pagar.

El hacker se ha aprovechado de este codigo para hacer crimen informaticos

los hacker tienen relacion con el -open source ellos Conocen lo fiables que son los engranajes de internet . Reemplazar el TCP/IP, DNS, Perl, Apache, etc., por el software Privativo sería, cuando menos, suicida.

Los conocidos hackers conocen el "open source" ,pero ellos temen ya que pueden ser penalizados por abusar, hay suficientes razones para pensar que ese temor es infundado.

Los famosos hackers tienen las posiblidades de luchar contra grandes organizaciones monopolizadas . el open source ofrece la oportunidad de que una persona posea un articulo que le es dificil obtenerlo por si mismo.tambien ofrece la posibilidad de hacer las correcciones a un programa ayudar al usuario. lleva a cabo la seguridad de programas.los codigos fuentes son publicosy está expuesto a millones de interezados.

Proyecto Final de Término - SEMÁFORO

Lógica TTL

Es una tecnología de construcción de circuitos electrónicos digitales.la entrada y salida del dispositivo son transistores bipolares.

Timer 555

El circuito integrado 555 es un circuito integrado de bajo coste y de grandes prestaciones. aplicaciones principales cabe destacar las de multivibrador estable y monoestable, detector de impulsos.

Contador

El contador es un circuito integrado, cada salida determinada un código de numero de pulsos que entran. tiene una serie de biestables conectados entre sí de tal forma que las salidas cambian de estado cuando se aplican impulso.

Circuito Or

Este es un dispositivo digital emite salida de bajo nivel cuando sus entradas son bajas, y una salida alta cuando existe por lo menos un alto en cualquiera de sus entradas o en las dos al mismo tiempo.

Funcionamiento del Proyecto Semáforo

Tabla de la verdad
E1 VERDE ROJO ROJO
E2 AMARILLO ROJO ROJO
E3 ROJO VERDE ROJO
E4 ROJO AMARILLO ROJO
E5 ROJO ROJO VERDE
E6 ROJO ROJO AMARILLO

Materiales Utilizados en nuestro Proyecto

Compuertas NOT·

Compuertas OR·

Compuertas NAND·

Diodos LED 5mm rojo, amarillo y verde·

Contador 7490·

Oscilador Lm555·

Switche pulsador·

Relé 5v·

Resistencias·

Cable UTP·

Pila 9v·

Lamina de anime·

Block de construcción·

Pega·

Cartulina blanca·

Barras de silicón·

Palitos chinos·

Pintura al frio·

Condensadores·

Protoboard

Observaciones

Cabe destacar que para la elaboración de este proyecto se conto con ciertos materiales las cuales ya antes han sido mencionados. Ante todo surgió la idea de poder visualizar de una manera más fácil y practica nuestro objetivo en programas las cuales nos permiten obtener una perspectiva en relación al comportamiento de este objeto.

Una vez realizado esto, pasamos a la parte practica que es la de montar los diferentes circuitos en un protoboard o tableta experimental.Este protoboard es una herramienta que nos facilita poder interconectar elementos electrónicos, ya sean resistencias, capacidades, semiconductores, etc. Sin la necesidad de soldar los componentes.

El protoboard está lleno de orificios metalizados con contactos de presión en los cuales se insertan las componentes del circuito a ensamblar.Luego pasamos a montar los componentes, teniendo como guía el circuito general del semáforo el cual pudimos obtener mediante la simulación del mismo, este nos permitió identificar cada unos de los diferentes elementos y conectarlos en su lugar correspondiente.

Sin embargo anterior a esto surgió la idea de montarlo en una placa de circuito impreso pero debido a ciertos inconvenientes, como por ejemplo: el tiempo que se toma para soldar cada uno de los componentes a diferencia que en el protoboard no existe esta necesidad, entre otros aspectos, omitimos esta opción.Para este proyecto se conto con la construcción de una maqueta con la finalidad de representar el funcionamiento real del semáforo, tomando como punto de referencia nuestro sitio de estudio, específicamente la Urbanización Llano Alto.

Podemos mencionar que a pesar de nuestros esfuerzos, no cumplimos con nuestra meta propuesta, esto ocurre gracias a la falta de experiencia en cuanto al manejo de circuitos integrados así mismo como en la manipulación del protoboard, ya que se nos presentaron múltiples inconvenientes dificultando así el alcance de nuestros objetivos.

OTRAS IMAGENES

Hacer Click sobre la Imgen para ver en tamaño Completo

Algebra de Boole

George Boole

George Boole nace el 2 de diciembre de 1815, en lincoln(inglaterra);aproximo la logica a una algebra simple, incorporando logica en las matematicas. su algebra consiste en metodos de resolucion de logica que tienen solo numeros binarios,es decir, 1 y 0.y a tres operadores:

and,or y not.

Y se le llamo algebra booleana,la cual ahora se le aplica en la contruccion de computadores y circuitos electricos.

Un día en el 1864 camino desde su casa al colegio, una distancia de dos millas, con una lluvia torrencial y luego dio una conferencia con la ropa empapada. El resultado fue un resfrío febril el cuál pronto dañó sus pulmones y terminó su carrera".

Función Lógica :

se le llama asi a toda variable binaria que tiene valor depende de una expresión formada por otras variables binarias relacionadas por los signos +(mas) y x(por).

ejemplificando:

S=(a.b)+b.c. Siendo S la función, a, b y c son las variables.

Postulados del Algebra de Boole

Propiedad Conmutativad:

a + b = b + a a . b = b . a

Identidad

0 + a = a 1 . a = a

Propiedad Distributiva

a . (b + c) = a . b + a . c a + b . c = (a + b) . (a + c)

Segundo Teorema

a+1=1

a.0=0

Tercer Teorema

a+a=a

a.a=a

Ley de Absorcion

a+a.b=a

a.(a+b)=a

Puertas Lógicas

Puerta And

Con esta se obtiene una salida de alto nivel, las entradas tienen que ser 1 para que la salida sea 1


Ejemplificando:


A=1 y B=1 entonces S=1

funcion: S=A.B

Simbolo:Puerta NAND

Esta se caracteriza por tener un nivel de salida bajo.cuando todas las entradas son 1 la salida es 0

Si A=1 y B=1 entonces S=0.

funcion : S= A.B (negados)
simbolo:

Puertas OR

siempre se obtiene 1 a la salida,cambia solo si las entradas son 0

S= A+B

simbolo: Puertas NOR

La salida es contraria a las puertas or.solo cuando se tenga nivel bajo en las entradas se obtendra nivel alto en las salidas.

S=A+B(negados)

Imprimir

Sistema de Numeracion

Los sistemas de numeracion comprenden dos tipos el secular decimal y el binario.

El sistema de numeracion decimal basicamente es un sistema posicional(depende de un simbolo llamado coma decimal"," y 9 digitos;"del 0 al 9")un solo digito puede variar su valor dependiendo de su posicion, utilizan como base "10"; esto se debe a la cantidad de digitos que utiliza,como ya lo digimos que van de "0 al 9".

Ejemplificando:

1000 mil
100 cien
10 diez
1 uno
0,1 un décimo
0,01 un centésimo

EL SISTEMA BINARIO

Ahora bien en este sistema solo se va a trabajar con dos digitos "0 y 1";esta numeracion se hizo con la finalidad de comunicarse el hombre con el harware, y se le llamo binario, ya que es de base 2(numeros de digitos en el sistema).

Ejemplificando:

Como múltiplos del bit:

8 bits " Byte (palabra) B (10110110)
1024 bytes " 1 kilobyte KB
1024 KB " 1 Megabyte MB
1024 MB " 1 Gigabyte GB
1024 GB " 1 Terabyte TB

En este sistemas de numeracion comprenden los sistemas(octal y hexadecimal).

Sistema Octal:

Se le llama asi debido a que su base es "8",es decir, que uiliza solo ocho simbolos para representar un valor cualquiera, estos numeros van desde el "0" al "7";si nos damos cuenta contando desde el "0" hasta el 7 hay 8 posiciones.

Ejemplificando:

0 1 2 3 4 5 6 7

Sistema Hexadecimal:

Se le llama asi debido a que es de base "16",utiliza 16 digitos para representar cualquier valor.

Ejemplificando:

0 1 2 3 4 5 6 7 8 9 A B C D E F

Ahora vamos a establecer la conversion entre estos tres sistemas:

Cuando hablamos de concersion entre los distintos sistemas nos referimos a la transformacion de un sistema equivlente en otro sistema.

Conversión decimal a binario

Para convertir un número decimal entero a binario, este debe ser dividido por dos y repetir el proceso con sus cocientes hasta que el cociente tome el valor 1. La unión de todos restos se tienen que tomar en orden inverso,es decir, el último cociente va a ser el primero.

Ejemplificando:


Convertir el número 174 a binario
17410 = 101011102

Conversión binario a decimal

se deben multiplicar cada digito por 2

Ejemplificando:

0 * 20 =0
1 * 21 =2
1 * 22 =4
1 * 23 =8
0 * 24 =0
1 * 25 =32
0 * 26 =0
1 * 27 =28

total =174
101011102 = 17410 este diez que aparece agregado a la cantidad no es mas que la representacion del sistema al cual es equivalente este valor,siendo el sistema decimal base 10.

Ahora bien en caso de que tenga pare entera y decimal se recomiensa el uso del torema fundamental de numeracion.

Ejemplificando:

Convertir 1101,0112 a base 10

Para pasar a base 10 deberemos hacer:

1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 + 0 * 2-1 + 1 * 2-2 + 1 * 2-3 =
1 * 8 + 1 * 4 + 0 + 1 * 1 + 0 + 1 * 0,25 + 1 * 0,125 =
8 + 4 + 0 + 1 + 0 + 0,25 + 0,125 = 13,375

1101,0112 = 13,37510

Conversión octal a binario

Cada digito octal sera reemplazado por 3 digitos binarios, se hace en forma directa digito a digito.

Ejemplificando:
Convertir a binario el número 276,5348

276,5348 = 10111110,10101112

Conversión binario a octal

Esta es similar a la anterior lo que varia es que a cada tres simbolos binarios le corresponde solo uno octal,pero para que se haga una conversion correcta es importante que sea multiplo de tres el resultado si no lo es se le agrega ceros..hasta que sea necesario tenerlo, esto es para la parte que esta a la izquierda de la coma","e identicamente a la parte derecha y se agrega al principio del numero.

Ejemplificando:

Convertir el binario 10101011,0011 a octal.

Conversión hexadecimal a binario

Identicamente comoen el caso anterior,la conversion se hace digito a digito, pero en este caso cada digito decimal sera reemplazado por 4 digitos binarios.

Ejemplificando:


Convertir a binario el número 5A8,39C16

5A8,39C16 = 10110101000,00111001112

Conversión binario a hexadecimal

Esta es similar a octal pero en lugar de tres, cuatros simbolos binarios le corresponden a solo1 hexadecimal, deben ser multiplos de 4 si no lo fuera, debera agregarseles cero.

Ejemplificando:

Convertir el binario 1010101011,00111 a hexadecimal
1010101011,00111 2 = 2AB,38816

Imprimir

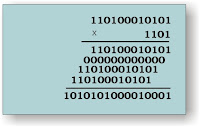
Operaciones Binarias

Suma

Sólo hay que recordar cuatro combinaciones posibles: Las sumas 0 + 0, 0 + 1 y 1+0;para ejemplificar mejor: 0 + 0 = 00 + 1 = 11 + 0 = 1 Ver siguiente ejercicio: 010 + 101 = 111 210 + 510 = 710110111011 + 100111011 = 1011110110 44310 + 31510 = 75810

Ejemplificando:

Sustracción

Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia;para ejemplicar ver el ejemplo siguiente:

0 – 0 = 01 – 0 = 11 – 1 = 0

Ejemplo de ejercicio resuelto:

111 – 101 = 010 710 – 510 = 210111101001 – 101101101 = 001111100 48910 – 36510 = 12410



Multiplicación

La Multiplicación binaria basicamente funciona igual a la multiplicacion decimal, la diferencia es que no existen las propiedades y solo se trabaja con dos digitos 0 y 1,es decir,en numeros binarios.

Ejemplificando:

División

Divisionlas divisiones binarias, las reglas son las mismas que en el Sistema Decimal, con la ventaja de que en binario sólo se usan dos dígitos,es decir 0 y 1.Para dividir 1100102 entre 102

se opera de la siguiente manera:

Imprimir

Analógico vs Digital

El termino digital se refiere a cantidades discretas como la cantidad de personas en un una sala, cantidad de libros en una biblioteca, cantidad de autos en una zona de estacionamiento mientras que el termino analogico se refiere a las magnitudes o valores que varían con el tiempo en forma continua como la distancia y la temperatura, la velocidad, que podrían variar muy lento o muy rápido.

reloj analogicoreloj digital

Como se puede observar el reloj analogico posee unas agujas mientras que el didital posee un display que muestra los numeros, estas señales son totalmente diferente la analogica no tiene forma definida mientras que la digital si es definida y se mantiene sobre el eje de las x;se puede ver claramente en las siguientes graficas:

Señal analogica Señal digital

imprimir

Karnaugh Map 1.2

Aqui les dejo un link de descarga de una aplicación pequeña pero sencilla sobre los Mapas de Karnaugh


http://www.puz.com/sw/karnaugh/kmap12.exe

suma de productos

Producto de Suma

maps de Karnauhg

puertas logicas

http://www.scribd.com/doc/2081783/Logica-boole-chip

Tutorial muy bueno .

Subido por: Mostafa Duerí

Circuitos Lógicos

Un computador es una serie de circuitos electrónicos que mediante el mecanismo de ejecución de instrucciones dan vida a una serie de operaciones que permiten, finalmente, ver lo que se ve al estar frente a la pantalla de uno de ellos y el poder interactuar, con ellos, de manera más o menos inteligente, dependiendo de lo que de ésta tenga el interactuante ya que se sabe que los computadores -como hoy se conocen- no tienen ni una pizca de inteligencia.

Básicamente un computador funciona mediante dos estados o valores conocidos como señales, por ejemplo, -1.5 volts y +4.0 volts. Estos voltajes tienen un significado lógico, con un valor se representa la existencia de una condición particular y el otro representa la ausencia de aquella condición. Para aclarar los conceptos anteriores, considere algo en el mundo que sólo puede tomar dos estados o posiciones o características, por ejemplo, una puerta que sólo puede estar abierta o cerrada, o el día y la noche o lo que es más preciso si una luz está prendida o apagada. Los casos descritos, exageradamente, pueden tener esa condición dual que es posible representar por estas señales, por ejemplo la señal -1.5 volt podría representar a "la puerta abierta", "al día", "a la luz encendida" y en cambio la señal de +4.0 volt podría representar el otro estado de los hechos: "la puerta cerrada", "la noche", "la luz apagada".

Operaciones Básicas
And. La operación And requiere que todas las señales sean simultáneamente verdaderas para que la salida sea verdadera. Así, el circuito de la figura necesita que ambos interruptores estén cerrados para que la luz encienda.

Figura No. 5. Operación And.
Los estados posibles del circuito se pueden modelar en la Tabla de Verdad que tiene asociada. Sabemos que los interruptores sólo pueden tener dos estados, abiertos o cerrados, si el interruptor abierto se representa mediante el cero (0 o falso) y el cerrado mediante el valor uno (1 o verdadero) entonces en la tabla de verdad asociada se puede ver la situación que se describía en el párrafo anterior, cuando se decía que la luz sólo prende cuando ambos interruptores están cerrados, es decir, si A = 1 y B = 1 entonces L = 1.
La compuerta lógica es una forma de representar la operación And pero en el ámbito de los circuitos electrónicos, para ese caso A y B son las señales de entrada (con valores = 0 1) y L es la señal de salida.
Para efectos de este curso, la operación And la representaremos como la función And( A, B ), donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = And( A, B ), correspondería a la forma de asignación de valor a L. En este caso el parámetro de salida es la misma función And.

Or. La operación Or tiene similares características a la operación And, con la diferencia que basta que una señal sea verdadera para que la señal resultante sea verdadera. En la figura se puede ver tal situación.


Figura No. 6. Operación Or.
Note que en el circuito los interruptores están en paralelo, por lo cual basta que uno de ellos esté cerrado para que el circuito se cierre y encienda la luz.

La operación Or también tiene una representación funcional como Or( A, B ) donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = Or( A, B ), correspondería a la forma de asignación de valor a L. En este caso, el parámetro de salida es la misma función Or.

Not: La última de la tres operaciones fundamentales, la cual también se conoce como negación, complemento o inversión, es mucho más simple que las anteriores. En la figura se puede observar el circuito, que en este caso tiene la particularidad de que al estar el interruptor abierto la luz enciende, cuando él está en posición de cerrado la luz permanecería apagada.



Figura No. 7. Operación Not.
La notación funcional para esta operación será Not( A ), donde A corresponde a la señal de entrada y Not( A ) corresponde al valor complementario de A.
Con las operaciones básicas ya definidas es posible redefinir el Algebra de una manera más formal, por ejemplo, dándole el nombre de Dominio Lógico y caracterizandolo de la siguiente manera:
Dominio Lógico ( l Î Dominio Lógico ) = ( { 0, 1 }, { l: And( l, l ), l:Or( l, l ), l:Not( l ) } )
Note que cada una de las operaciones o funciones de este dominio se ha explicitado claramente la cantidad y el tipo de parámetros con los cuales ellas operan (operandos) y el tipo de valor que la operación devuelve, en este caso todos los parámetros son del tipo lógico ( l ).
Así, cuando se habla del dominio del computador al resolver un problema, este dominio tiene como base el dominio recién descrito. Los circuitos electrónicos que dan vida al computador pueden ser representados todos mediante este Dominio Lógico.


Para mas Información visite: Circuitos Lógicos

Publicado por: Luis G. Díaz R.

Da click para Imprimir